A Tale of Two Molecules: How the Heat Capacities of N\(_2\)(g) and F\(_2\)(g) Differ At High Temperature and Why Naïve Expectations Fail to Explain These Differences: A Spreadsheet Exercise for Physical Chemistry Students
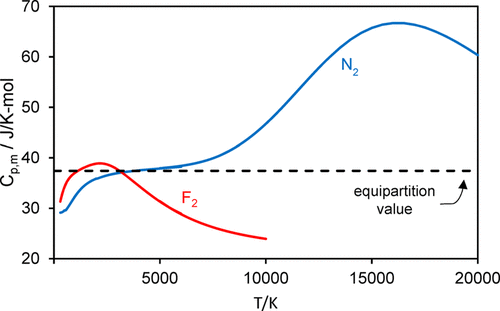
A spreadsheet-based exercise for students is described in which they are challenged to explain and reproduce the disparate temperature dependencies of the heat capacities of gaseous F\(_2\) and N\(_2\). For F\(_2\), C\(_{p,m}\) increases from 300 K, reaches a maximum at 2200 K, and then decreases to 74% of the maximum value at 6000 K, while C\(_{p,m}\) for N\(_2\) rises monotonically in this temperature range. Students compare this behavior with the prediction of the equipartition principle and then test four models with increasing sophistication, from closed-form expressions of the harmonic/anharmonic oscillator–rigid/nonrigid rotor to calculations using discrete sums over rovibrational states, all using molecular spectroscopic constants. Fundamental principles of statistical thermodynamics are used to calculate the partition functions, which yield the internal energy, heat capacity, and third-law entropy of the molecules. They encounter the need to include the role of quasibound rotational states that arise from the rotational barrier to molecular dissociation and to employ methods for truncating the sums used in the partition functions. In this exercise, students confront the fact that, for N\(_2\), C\(_{p,m}\) continues to rise, reaching a maximum at 16,000 K that is 1.8 times the equipartition value. The inclusion of electronically excited states in the partition function is discussed.
Citation
J. Chem. Educ. 2019, 96, 5, 926–935
License
Copyright 2019 American Chemical Society and Division of Chemical Education, Inc.